I basically agree with Chase's answer - with some additions. But let's see thoroughly what is behind that sentence in Wikipedia ("Most steel engines have a thermodynamic limit of 37%").
Internal combustion engines are modeled by the Otto cycle rather than by the Carnot cycle. Looking at this link for the Otto cycle (or this great link from MIT), you may observe that in this cycle there are four temperatures involved, and the efficiency is given by
$$ \epsilon_O = 1-\frac{T_4- T_1}{T_3 - T_2}. $$
However, in an ideal Otto cycle we have that $T_4/T_1 = T_3/T_2$, and we get an "effective Carnot form" for the efficiency:
$$ \epsilon_O = 1-\frac{T_1}{T_2}. $$
Now, using the isentropic equations of ideal gases, we obtain the following simple expression
$$ \epsilon_O = 1- \frac{1}{(V_1/V_2)^{\gamma -1}}, $$
where $\gamma$ is the specific heat ratio ($c_p/c_v$)
At the end of the Wikipedia sentence that you quote, there is a reference to a course by the University of Washington (see link here). There it is stated that most current auto engines have compression ratio $V_1/V_2=10$ and the mixture of air, gasoline vapor, CO$_2$, CO and H$_2$O has an effective specific heat ratio of $\gamma=1.27$. Plugging this into our formula we get $\eta_O=0.46=46\% $, which is pretty close to what Chase said. I would call this the theoretical limit for the efficiency of the internal combustion engine!
But how do they get $35-37\%$ instead? Here I have to quote the Uni of Washington link directly:
(...) you get h = 0.46. Multiply this by about 0.75 to account for real cycle effects (such as the time it takes to burn, heat losses to the coolant, and exhaust valves that open before the piston fully reaches bottom position) and you have h = 0.35.
So in conclusion, after a careful look through the different links, I have to agree with Chase (with the above described additions), the efficiency limit dictated by thermodynamics is ~46%, and the 35% limit arrives when additional real-life considerations are taken into account. Although admittedly this "let's multiply by 0.75" approach does not sound very well grounded on its own. But at least it answers your question "where this number comes from".
RELATED VIDEO



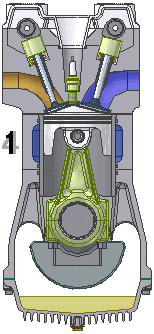 The internal combustion engine is an engine in which the combustion of a fuel (normally a fossil fuel) occurs with an oxidizer (usually air) in a combustion chamber that is an integral part of the working fluid flow circuit. In an internal combustion engine, the...
The internal combustion engine is an engine in which the combustion of a fuel (normally a fossil fuel) occurs with an oxidizer (usually air) in a combustion chamber that is an integral part of the working fluid flow circuit. In an internal combustion engine, the...
 Fuel usage in automobiles refers to the fuel efficiency relationship between distance traveled by an automobile and the amount of fuel consumed.
Fuel usage in automobiles refers to the fuel efficiency relationship between distance traveled by an automobile and the amount of fuel consumed.







