Chapter 11: Combustion
(Thanks to for his assistance in writing this section)
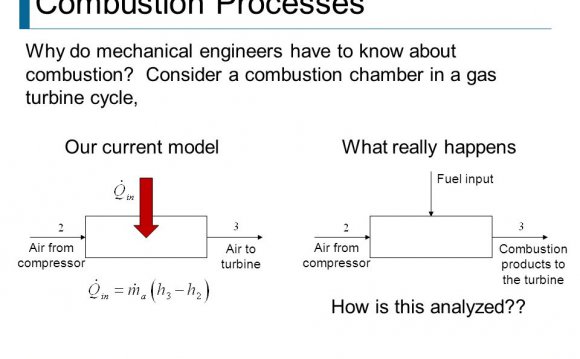
Introduction - Up to this point the heat Q in all problems and examples was either a given value or was obtained from the First Law relation. However in various heat engines, gas turbines, and steam power plants the heat is obtained from combustion processes, using either solid fuel (e.g. coal or wood). liquid fuel (e.g. gasolene, kerosine, or diesel fuel), or gaseous fuel (e.g. natural gas or propane).
In this chapter we introduce the chemistry and thermodynamics of combustion of generic hydrocarbon fuels - (CxHy), in which the oxydizer is the oxygen contained in atmospheric air. Note that we will not cover the combustion of solid fuels or the complex blends and mixtures of the hydrocarbons which make up gasolene, kerosene, or diesel fuels.
Atmospheric Air contains approximately 21% oxygen (O2) by volume. The other 79% of "other gases" is mostly nitrogen (N2), so we will assume air to be composed of 21% oxygen and 79% nitrogen by volume. Thus each mole of oxygen needed to oxidize the hydrocarbon is accompanied by 79/21 = 3.76 moles of nitrogen. Using this combination the molecular mass of air becomes 29 [kg/kmol]. Note that it is assumed that the nitrogen will not normally undergo any chemical reaction.
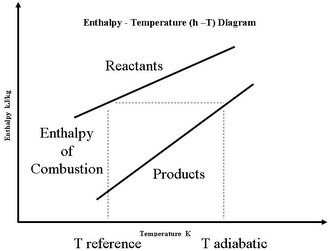
The Combustion Process - The basic combustion process can be described by the fuel (the hydrocarbon) plus oxydizer (air or oxygen) called the Reactants, which undergo a chemical process while releasing heat to form the Products of combustion such that mass is conserved. In the simplest combustion process, known as Stoichiometric Combustion, all the carbon in the fuel forms carbon dioxide (CO2) and all the hydrogen forms water (H2O) in the products, thus we can write the chemical reaction as follows:
where z is known as the stoichiometric coefficient for the oxidizer (air)
Note that this reaction yields five unknowns: z, a, b, c, d, thus we need five equations to solve. Stoichiometric combustion assumes that no excess oxygen exists in the products, thus d = 0. We obtain the other four equations from balancing the number of atoms of each element in the reactants (carbon, hydrogen, oxygen and nitrogen) with the number of atoms of those elements in the products. This means that no atoms are destroyed or lost in a combustion reaction.
| Element | Amount in reactants | Amount in Products | Reduced equation | |
| Carbon (C) | a = x | |||
| Hydrogen (H) | 2b | b = y/2 | ||
| Oxygen (O) | 2z | 2a+b | z = a + b/2 | |
| Nitrogen (N) | 2(3.76)z | 2c | c = 3.76z |
Note that the water formed could be in the vapor or liquid phase, depending on the temperature and pressure of the combustion products.
As an example consider the stoichiometric combustion of methane (CH4) in atmospheric air. Equating the molar coefficients of the reactants and the products we obtain:
Theoretical Air and Air-Fuel Ratio -The minimum amount of air which will allow the complete combustion of the fuel is called the Theoretical Air (also referred to as Stoichiometric Air). In this case the products do not contain any oxygen. If we supply less than theoretical air then the products could include carbon monoxide (CO), thus it is normal practice to supply more than theoretical air to prevent this occurrence. This Excess Air will result in oxygen appearing in the products.
The standard measure of the amount of air used in a combustion process is the Air-Fuel Ratio (AF), defined as follows:
Thus considering only the reactants of the methane combustion with theoretical air presented above, we obtain:
Solved Problem 11.1 - In this problem we wish to develop the combustion equation and determine the air-fuel ratio for the complete combustion of n-Butane (C4H10) with a) theoretical air, and b) 50% excess air.
Analysis of the Products of Combustion - Combustion always occurs at elevated temperatures and we assume that all the products of combustion (including the water vapor) behave as ideal gases. Since they have different gas constants, it is convenient to use the ideal gas equation of state in terms of the universal gas constant as follows:
In the analysis of the products of combustion there are a number of items of interest:
- 1) What is the percentage volume of specific products, in particular carbon dioxide (CO2) and carbon monoxide (CO)?
- 2) What is the dew point of the water vapor in the combustion products? This requires evaluation of the partial pressure of the water vapor component of the products.
- 3) There are experimental methods of volumetric analysis of the products of combustion, normally done on a Dry Basis, yielding the volume percentage of all the components except the water vapor. This allows a simple method of determining the actual air-fuel ratio and excess air used in a combustion process.
For ideal gases we find that the mole fraction yi of the i'th component in a mixture of gases at a specific pressure P and temperature T is equal to the volume fraction of that component.
Since from the molar ideal gas relation: P.V = .T, we have:
Furthermore, since the sum of the component volumes Vi must equal the total volume V, we have:
RELATED VIDEO


 Combustion ( /kəmˈbʌs.tʃən/) or burning is the sequence of exothermic chemical reactions between a fuel and an oxidant accompanied by the production of heat and conversion of chemical species. The release of heat can result in the production of light in the form of...
Combustion ( /kəmˈbʌs.tʃən/) or burning is the sequence of exothermic chemical reactions between a fuel and an oxidant accompanied by the production of heat and conversion of chemical species. The release of heat can result in the production of light in the form of...
 Chemical thermodynamics is the study of the interrelation of heat and work with chemical reactions or with physical changes of state within the confines of the laws of thermodynamics. Chemical thermodynamics involves not only laboratory measurements of various...
Chemical thermodynamics is the study of the interrelation of heat and work with chemical reactions or with physical changes of state within the confines of the laws of thermodynamics. Chemical thermodynamics involves not only laboratory measurements of various...








