Where Q is the heat released per pound of fuel which depends on the fuel, f is the fuel/air ratio for combustion which depends on several factors associated with the design and temperature in the combustion chamber, and cv is the specific heat at constant volume. From the equation of state, we know that:
p4 = p3 * (T4 /T3)
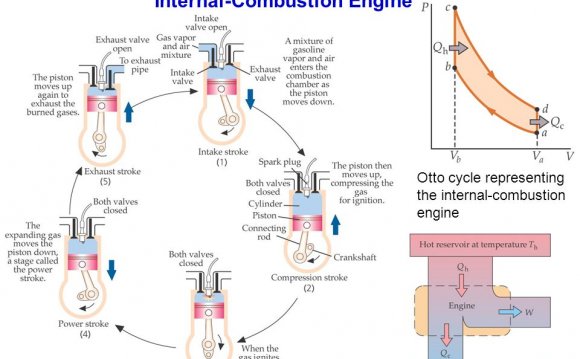
During the power stroke (4-5), work is done by the gas on the piston. The expansion ratio is the reciprocal of the compression ratio and we can use the same relations used during the compression stroke:
p5 / p4 = r ^ (-gamma)
T5 / T4 = r ^ (1 - gamma)
During the cycle, work is done on the gas by the piston between stages 2 and 3. Work is done by the gas on the piston between stages 4 and 5. The difference between the work done by the gas and the work done on the gas is shown in yellow and is the work produced by the cycle. We can calculate the work by determining the area enclosed by the cycle on the p-V diagram. But since the processes 2-3 and 4-5 are curves, this is a difficult calculation. We can also evaluate the work by the difference of the heat into the gas minus the heat rejected by the gas. Knowing the temperatures, this is an easier calculation.
W = cv * [(T4 - T3) - (T5 - T2)]
The work times the rate of the cycle (cycles per second cps) is equal to the power P produced by the engine.
P = W * cps
On this page we have shown an ideal Otto cycle in which there is no heat entering (or leaving) the gas during the compression and power strokes, no friction losses, and instantaneous burning occurring at constant volume. In reality, the ideal cycle does not occur and there are many losses associated with each process. These losses are normally accounted for by efficiency factors which multiply and modify the ideal result. For a real cycle, the shape of the p-V diagram is similar to the ideal, but the area (work) is always less than the ideal value.
RELATED VIDEO



 Physical chemistry is the study of macroscopic, atomic, subatomic, and particulate phenomena in chemical systems in terms of laws and concepts of physics. It applies the principles, practices and concepts of physics such as motion, energy, force, time...
Physical chemistry is the study of macroscopic, atomic, subatomic, and particulate phenomena in chemical systems in terms of laws and concepts of physics. It applies the principles, practices and concepts of physics such as motion, energy, force, time...








